石器时代当攻防双方没有任何buff而且不暴击时有的规律

今天我们在石器时代可以总结出第一个趋势方程：

当攻防双方没有任何buff而且不暴击时，有以下规律：

1. 趋势方程：当攻击力明显大于防御力时，伤害=攻击力X 1.7 – 防御力X 1.4，浮动区间一般不超过正负10%左右。

2. 当攻击力接近或小于防御力时，伤害值会比上述公式低，随着差距扩大，逐步趋向于上述方程。

3. 当攻击力小于防御力的88%左右时，会表现出不破防，伤害=总攻击力X 0.1。

接下来是计算过程：

发帖上次之后，我做了4轮实验。

当总防御力不变，为4848时，破防后，伤害值随着攻击力成线性变化，趋势曲线方程为：

伤害=总攻击力X1.7054 – 7127 （防御力=4848）；

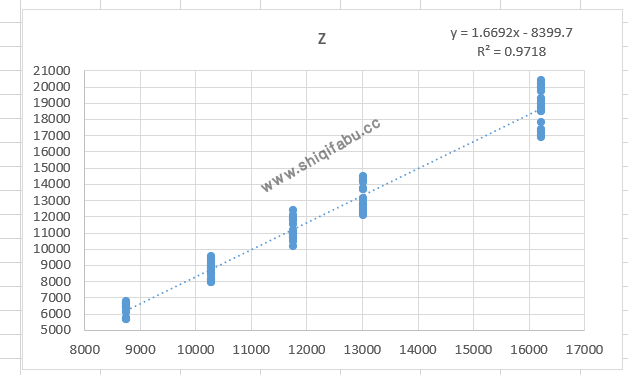
当总防御力不变，为6074时，破防后，伤害值随着攻击力成线性变化，趋势曲线方程为：

伤害=总攻击力X1.6692 – 8299.7 （防御力=6074）；

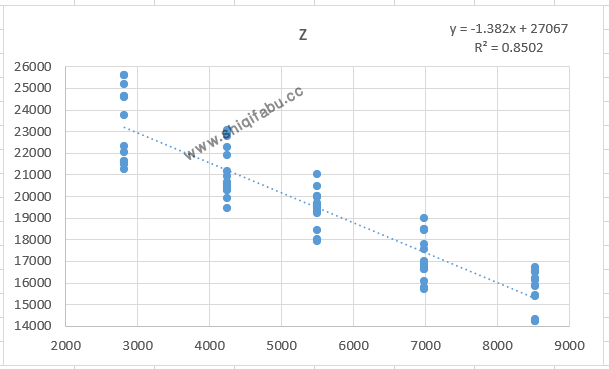
当总攻击力力不变，为16222时，破防后，伤害值随着攻击力成线性变化，趋势曲线方程为：

伤害=27067 – 防御力X 1.382 （攻击力=16222）；

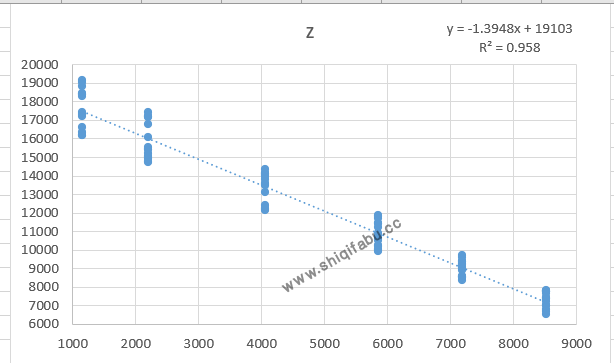
当总攻击力力不变，为11357时，破防后，伤害值随着攻击力成线性变化，趋势曲线方程为：

伤害=19103 – 防御力X 1.3948 （攻击力=11357）；

我们可以发现：

1. 防御力不变，且在攻击力明显大于防御力时，伤害结算的趋势方程与攻击力线性正相关，但防御力越高时，攻击力的系数越小。

2. 攻击力不变，且在攻击力明显大于防御力时，伤害结算的趋势方程与防御力线性负相关，但攻击力越高时，防御力的系数越小。

首先，我假设这个系数变动是因为样本误差，那么可以认为伤害结算公式为：

Z=K1X+K2Y+K3；

其中Z为伤害，

X为防御力，

Y为攻击力，

K3为常数，

K1为负数。

这是一个空间平面方程，在这种情况下，我们可以使用最小二乘法求最小误差：

n组数据的（Zi – （K1Xi+K2Yi+K3））平方，分别以K1，K2，K3为变量，以这个公式的最小值（即使误差最小）时，K1，K2，K3的值作为我们的系数。

但计算大半天后，数据还是十分不对路，所以我暂时认为这个假设不成立。

Z=K1X+K2Y+K3；

其中Z为伤害，

X为防御力，

Y为攻击力，

K1，K2，K3大概率不是常数，而是随着X和Y在变化，这个方程大概是一个空间曲面。

那么退而求其次，既然伤害值是一个区间内的随机变量，我们暂时用一个相对简单的近似方程来表达这个结算的规律。

就是Z=1.7Y-1.4X，但当攻击力接近或稍微小于防御力时，这个近似方程的误差会被放大，伤害会比公式算的稍微低一些（攻击力系数下降/防御力系数上升）。

至于最准确的方程，还是容我休息一下换换思路，改天再试试求解。

至于攻击力小于等于防御力的88%左右时，完全不破防，这是非常简单的夹逼法做得测试。

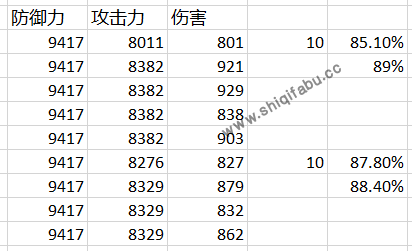
在几组不同的防御力和攻击力组合上，当攻击力小于防御力的88%左右时，会出现伤害=攻击力x0.1的完全不破防现象。

以上，谢谢观看，啾咪。